Assessment of the health impacts of H1N1 vaccination

This page is a knowledge crystal of subtype assessment. The page identifier is Op_en4926
Moderator:Teemu R (see all)
Upload data {{#opasnet_base_link:Op_en4926}}

Main message:

Question: What was the overall health impact of the H1N1 (swine flu) vaccination in Finland in 2009-2010? Given current knowledge, which was the better decision between vaccinating as happened versus vaccinating no-one versus not vaccinating the population aged 5-19? Answer: Given current knowledge, the decision to vaccinate the whole population was the best decision even when narcolepsy is included in the assessment. Results of the Value of information analysis suggest that further knowledge about the uncertain variables considered very likely would not have changed the decision.

This assessment calls for new participants to work on this important topic.

Opasnet is a web-workspace for improving decision-making by collecting and distributing important knowledge. It is based on the work by a large group of interested and active volunteers who want to make a difference. If you are interested, please add your username under the Participants heading. Make also sure that My preferences of your account contain a valid email address for you, so that other Opasnet users can contact you (the email is not disclosed to other users).

This assessment is about the total health effects the 2009 swine flu pandemic. It utilizes data from the Infectious disease registry (TTR) maintained by THL, the National narcolepsy task force report from 31.1.2011 and WHO. The current model is a simplification with no time dimension.

Scope

• What was the overall health impact of the H1N1 vaccination in Finland in 2009-2010?
• Given current knowledge, which was the better decision between vaccinating as happened versus vaccinating no-one versus not vaccinating the population aged 5-19?
• Monetary impact is not considered.

Participants

• THL: Virpi Kollanus, M.Sc., Marko Tainio, Ph.D., Mikko V. Pohjola, M.Tech.Sci., Jouni T. Tuomisto, M.D., Dr.Med.Sci., Teemu Rintala
• This is an open assessment. Anyone can participate.

Result

{{#opasnet_base_link:Op_en4926}}

Results

Distributions of the results for the different scenarios/decisions.

Comparison between scenarios and outcomes; onarc is DALYs from narcolepsy, osf is DALYs from having swine flu and osfm is DALYs from swine flu related mortality.

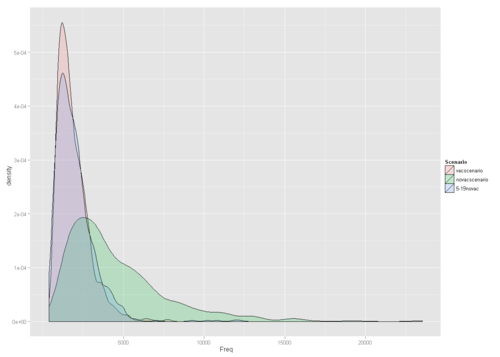
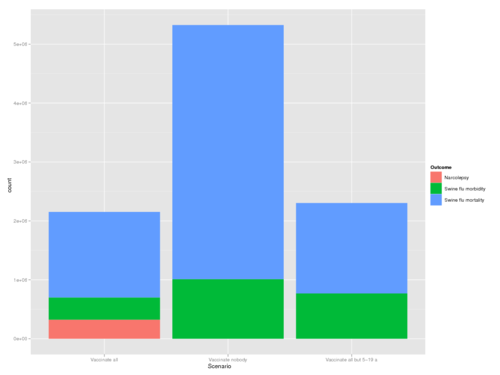
• From initial results it would appear like swine flu is more significant than narcolepsy in terms of DALYs.
  • Vaccinating as planned would result in approximately 1850 DALYs due to swine flu and narcolepsy combined.
  • Vaccinating no-one would result in approximately 4400 DALYs due to swine flu.
  • Vaccinating everyone but people aged 5-19 would result in about a total of 2000 DALYs.

• Probability of swine flu variable is revealed by both the sensitivity- and Value of information-analyses to have the most impact on the outcome.
  • The VOI analysis also reveals that further knowledge about the uncertain variables in the model is only worth up to ~80 DALYs, when considering the decision by age group, and less than 1 DALY when considering the decision as on/off as defined in the decision variable above. Which is only a small fraction of the total DALYs.

• Suggested statement: Pandemrix should not be used any more anywhere because its narcolepsy risk is too high.
  • Resolution: Not accepted. Pandemrix is still an effective and safe vaccine. However, due to precautionary reasons, other alternatives should be used when available, because the occurrence of narcolepsy is not understood. R↻

Conclusions

Given current knowledge, the decision to vaccinate the whole population was the best decision. Results of the Value of information analysis suggest that further knowledge about the uncertain variables considered very likely would not have changed the decision. The total impact of the swine flu pandemic and related narcolepsy cases in Finland in terms of DALYs is slightly smaller than that of radon (~6700 DALYs yearly) and slightly larger than that of moisture damage (~650 DALYs yearly) for instance. It should be noted that only three variables had their uncertainty taken into account, although they should represent the major uncertainties present. Also, herd immunity is assumed not to affect the probability of a non immune subject to catch swine flu, this results in an underestimation of the number of swine flu cases in scenarios where the vaccination coverage is less than what was observed.

Rationale

Causal diagram.

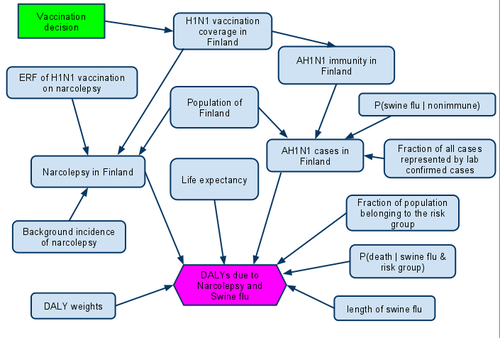
Decisions

• Vaccination decision
  • Vaccinate everyone (observed vaccination coverage)
  • Vaccinate no-one (0 vaccination coverage)

Variables

• H1N1 vaccination coverage in Finland
• ERF of H1N1 vaccination on Narcolepsy
  • Assumed lognormally distributed
• A(H1N1)v immunity in the Finnish population
  • P(immune) = 1 - P(not vaccinated) * P(no base immunity)
• Population of Finland
• Disability weights
  • DALY weight of narcolepsy equals roughly that of epilepsy (0.065)
  • DALY weight of having swine flu assumed ~0.5
• Life expectancy by age groups in Finland
• Probability of catching swine flu given subject is not immune
  • Estimated from data available (population, total immunity, number of cases) by fitting the number of cases to a poisson distribution and calculating probability from the mean estimate by dividing by the non-immune population
• Fraction of all cases represented by lab confirmed cases (which we have data on)
  • Estimated as beta-distributed with mean of 0.2 and some sd
• Probability of death due to swine flu given a subject has swine flu and belongs to a risk group
  • Estimated from data available
  • Assumed all deaths will be lab confirmed cases
  • Assumed that all deaths belonged to a risk group (had some base condition)
• Fraction of population belonging to a risk group
  • Arbitrary values; trying to account for kids of age <1 and old folks with heart conditions etc.
• Length of swine flu
  • Assumed to be flat 5 days (mildly incapacitated for this duration)
• Narcolepsy in Finland
• AH1N1 cases in Finland

Indicators

• DALYs from narcolepsy caused by vaccination
• DALYs from having swine flu
• DALYs from deaths caused by swine flu

R code

• Basic model
  • Uncertainties of ERF of vaccine on narcolepsy, fraction of all cases represented by lab confirmed cases and probability of catching swine flu are implemented.

+ Show code- Hide code # Model; original data inputs are disability weights (isfw, inarcw), population (ipop/dpop), (atm) ERF of vaccine on narcolepsy (NERF), # vaccination coverage (ivac_cov), base immunity in the population (ibimm) and observed number of sf cases (dsf) # i in the beginning of the name of an object signifies 'input', d signifies 'data' and t signifies 'temporary' # Function for aggregating indicators into DALYs. At the moment _narcolepsy cases_ and _swine flu cases_ are considered indicators, # however mortality due to swine flu should also be considered and indicator and calculated separately from this function. # Narcolepsy DALY weight taken as 0.065 (that of treated epilepsy) # iEl is expectation of remaining life in an age group, value for "All" is arbitrary for now # ilsf is the length of swine flu (e.g. how long was the subject absent frow work) in years # ifrg is the fraction of population belonging to a risk group of dying from swine flu, default values are arbitrary # iElrgc is the expected life correction for the risk group (people with heart conditions etc are likely to die earlier anyway) outcome <- function(inarc = narc(), isf = sf(), inarcw = data.frame(Result=0.065),#op_baseGetData("opasnet_base", "Op_en2307")[,-c(1,2)], isfw = data.frame(Result=0.5), iEl = data.frame(Age=c("0-4 ","5-9","10-14","15-19","20-24","25-29","30-34","35-39","40-44","45-49", "50-54","55-59","60-64","65-69","70-74","75-79","80+","All"), Result = c(79,75.1,70.1,65.1,60.3,55.5,50.7,45.9,41.1,36.5,31.9,27.6, 23.5,19.5,15.7,12.1,9,50)), ilsf = data.frame(Result=5/365), isfpd = sfpd(), ifrg = data.frame(Age = c("0-4 ","5-9","10-14","15-19", "20-24","25-29","30-34","35-39","40-44","45-49","50-54","55-59","60-64","65-69","70-74","75-79","80+"), Result = c(0.1, rep(0.001, 11), rep(0.5,5))), iElrgc = data.frame(Age = c("0-4 ","5-9","10-14","15-19","20-24","25-29","30-34","35-39","40-44","45-49","50-54", "55-59","60-64","65-69","70-74","75-79","80+"), Result = c(rep(1,12), rep(0.5,5))), ...) { names(inarc)[names(inarc)=="Result"] <- "inarc" names(inarcw)[names(inarcw)=="Result"] <- "inarcw" names(isf)[names(isf)=="Result"] <- "isf" names(isfw)[names(isfw)=="Result"] <- "isfw" names(iEl)[names(iEl)=="Result"] <- "iEl" names(ilsf)[names(ilsf)=="Result"] <- "ilsf" names(isfpd)[names(isfpd)=="Result"] <- "isfpd" names(ifrg)[names(ifrg)=="Result"] <- "ifrg" names(iElrgc)[names(iElrgc)=="Result"] <- "iElrgc" # Calculating narcolepsy DALYs onarc <- merge(inarc, inarcw) onarc <- merge(onarc, iEl) onarc <- model.frame(I(inarc * inarcw * iEl) ~., data = onarc) colnames(onarc)[1] <- "onarc" # Calculating swine flu DALYs from missing work osf <- merge(isf, isfw) osf <- merge(osf, ilsf) osf <- model.frame(I(isf * isfw * ilsf) ~., data = osf) colnames(osf)[1] <- "osf" #Calculating swine flu DALYs from deaths osfm <- merge(isf, isfpd) osfm <- merge(osfm, iEl) osfm <- merge(osfm, ifrg) osfm <- merge(osfm, iElrgc) osfm <- model.frame(I(isf * isfpd * iEl * ifrg * iElrgc) ~., data = osfm) colnames(osfm)[1] <- "osfm" # Aggregate (it is crucial that both variables are distinguished by the same age groups and other indices so that values # are not replicated to fill empty cells) out <- merge(onarc, osf) out <- merge(out, osfm) out <- reshape(out, idvar = names(out)[(names(out)%in%c("onarc","osf","osfm"))==FALSE], times = c("onarc","osf","osfm"), timevar = "Outcome", varying = list(c("onarc","osf","osfm")), direction = "long") colnames(out)[ncol(out)] <- "Result" rownames(out) <- 1:nrow(out) return(out) } # Function for calculating narcolepsy cases, depends on erf of vac on narc, pop, vac_cov and background incidence (fraction) narc <- function(iNERF = op_baseGetData("opasnet_base", "Op_en4923")[,-c(1)], ipop = op_baseGetData("opasnet_base", "Op_en2949")[,-c(1,2)], ivac_cov = op_baseGetData("opasnet_base", "Op_en4925")[,-c(1,2)], ibgi = data.frame(Result=1.4e-5), ...) { names(iNERF)[names(iNERF)=="Result"] <- "iNERF" names(ipop)[names(ipop)=="Result"] <- "ipop" names(ivac_cov)[names(ivac_cov)=="Result"] <- "ivac_cov" names(ibgi)[names(ibgi)=="Result"] <- "ibgi" out <- merge(iNERF, ipop) out <- merge(out, ivac_cov) out <- merge(out, ibgi) out <- model.frame(I((iNERF - 1) * ipop * ivac_cov * ibgi) ~., data = out) colnames(out)[1] <- "Result" return(out) } # A function for calculating NERF might be added later # Function for calculating swine flu cases # ilcf is the fraction of actual swine flu cases represented by the lab confirmed cases # (scrapped)assumed binomially distributed, if uncertainty of probability of getting swine flu is not # present, the point estimate will be used as such and n samples sampled from the same distribution; # however if the probability has an uncertainty, only 1 sample from each distribution is sampled where # samples of the probability will be used as inputs;(/scrapped) disabled sampling here since it would make different scenarios incomparable sf <- function(isfp = sfp(), ipop = op_baseGetData("opasnet_base", "Op_en2949")[,-c(1,2)], iimm = imm(), n = 1000, ilcf = tlcf, ...) { names(isfp)[names(isfp)=="Result"] <- "isfp" names(ipop)[names(ipop)=="Result"] <- "ipop" names(iimm)[names(iimm)=="Result"] <- "iimm" names(ilcf)[names(ilcf)=="Result"] <- "ilcf" out <- merge(isfp, ipop) out <- merge(out, iimm) out <- merge(out, ilcf) #Result <- NA #for (i in 1:nrow(out)) { # if (sum(as.numeric(colnames(isfp)=="obs"))>0){ # Result[i] <- rbinom(1, round(out$ipop[i]*(1-out$iimm[i])), out$isfp[i]) / out$ilcf[i] # } else { # Result[((i-1)*n + 1):(i*n)] <- rbinom(n, round(out$ipop[i]*(1-out$iimm[i])), out$isfp[i]) / out$ilcf[i] # } #} #out <- data.frame(out[,(colnames(out)%in%c("isfp","ipop","iimm","ilcf"))==FALSE], Result) out <- model.frame(I(isfp * ipop * (1 - iimm) / ilcf) ~., data = out) colnames(out)[1] <- "Result" return(out) } # Function for calculating probability of getting swine flu given subject is not vaccinated (simplified model) # dsf, dpop and dimm are the actual data we have # uncertainty: number of cases is binomially distributed, number of trials (n) is the number of people who were not immune to swine-flu # outcome x is known, p is unknown. P can be easily calculated from x = p*n, when we assume that x is the expected value of the # distribution. But we're interested in the uncertainty of the estimate... When n is suitably large a poisson distribution becomes # an excellent approximation of the binomial distribution. So we can fit the poisson distribution using an R function (I didn't find # one for binomial) from just one observation -> acquire value of x with standard error -> use as uncertainty of estimate; which produces # rubbish because we only have a single observation, sd of the mean estimate of the poisson distribution appears to be (n*p)^0.5, so the # variance of the parameter is n * p, which divided by n gives p ... so the expected value is p and the variance is p, which causes problems # with the beta distribution (shape parameters become negative), so I've used standard error^4 as the variance... # Somebody with real knowledge about these things should check this sometime, I'm just playing around with some numbers to get more # uncertainty in the model. sfp <- function(dsf = op_baseGetData("opasnet_base", "Op_en4933")[,-c(1,2)], dpop = op_baseGetData("opasnet_base", "Op_en2949", series_id = 970)[,-c(1,2)], dimm = imm(), n = 1000, ...) { names(dsf)[names(dsf)=="Result"] <- "dsf" names(dpop)[names(dpop)=="Result"] <- "dpop" names(dimm)[names(dimm)=="Result"] <- "dimm" temp1 <- merge(dimm, dpop) temp1 <- model.frame(I(dpop * (1 - dimm)) ~., data = temp1) colnames(temp1)[1] <- "popnonimm" out <- merge(temp1, dsf) temp2 <- data.frame(obs=NA, Age=NA, fitp=NA) out2 <- data.frame() for (i in 1:nrow(out)) { temp2 <- data.frame(obs=1:n, Age=out$Age[i], fitp=rbeta(n, paralpha(fitdistr(round(out$dsf[i]), "poisson")[[1]] / out$popnonimm[i], (fitdistr(round(out$dsf[i]), "poisson")[[2]]^2 / out$popnonimm[i])^2), parbeta(fitdistr(round(out$dsf[i]), "poisson")[[1]] / out$popnonimm[i], (fitdistr(round(out$dsf[i]), "poisson")[[2]]^2 / out$popnonimm[i])^2))) out2 <- rbind(out2, merge(out[i,], temp2, all.x = TRUE, all.y = FALSE)) } out2 <- out2[,(colnames(out2)%in%c("dsf", "popnonimm"))==FALSE] colnames(out2)[ncol(out2)] <- "Result" return(out2) } # Function for calculating probability of mortality after catching swine flu given that the subject belongs to a risk group # children of age < 1 and adults of 60+ afflicted by heart conditions etc are considered to belong to a risk group # ifrg is the fraction belonging to the risk group in a given age group # p(death|sf&rg)) assumed constant in all age groups # dsf is the data we have on the number of swine flu cases, dmsf is the data on mortality caused by swine flu, dfrg is the data on # the fraction of population belonging to risk groups (arbitrary default values included) sfpd <- function(dsf = op_baseGetData("opasnet_base", "Op_en4933")[,-c(1,2)], dmsf = data.frame(Result=44), dfrg = data.frame(Age = c("0-4 ","5-9","10-14","15-19","20-24","25-29","30-34","35-39","40-44","45-49", "50-54","55-59","60-64","65-69","70-74","75-79","80+"), Result = c(0.1, rep(0.001,11), rep(0.5,5))), ilcf = tlcf, ...) { names(dsf)[names(dsf)=="Result"] <- "dsf" names(dmsf)[names(dmsf)=="Result"] <- "dmsf" names(dfrg)[names(dfrg)=="Result"] <- "dfrg" names(ilcf)[names(ilcf)=="Result"] <- "ilcf" out <- merge(dsf, dfrg) out <- merge(out, ilcf) #out <- merge(out, dmsf) out <- model.frame(I(dfrg * dsf / ilcf) ~., data = out) colnames(out)[1] <- "Result" if (sum(as.numeric(colnames(out)=="obs"))>0) {#out <- as.data.frame(as.table(tapply(out$))) out <- data.frame(obs = levels(factor(out$obs)), Result = dmsf$dmsf/tapply(out$Result, out$obs, sum)) } else {out <- data.frame(Result=dmsf$dmsf/sum(out$Freq))} return(out) } # Function for calculating total immunity to swine flu in the whole population # P(imm) = P(vac or base_imm) # ibimm is the input background immunity # ivac_cov is the input vaccination coverage imm <- function(ibimm = op_baseGetData("opasnet_base", "Op_en4943", series_id = 994)[,-c(1,2)], ivac_cov = op_baseGetData("opasnet_base", "Op_en4925")[,-c(1,2)], ...) { names(ibimm)[names(ibimm)=="Result"] <- "ibimm" names(ivac_cov)[names(ivac_cov)=="Result"] <- "ivac_cov" out <- merge(ibimm, ivac_cov) out <- model.frame(I(1 - (1 - ibimm) * (1 - ivac_cov)) ~., data = out) colnames(out)[1] <- "Result" return(out) } ## Calculating the outcome with different scenarios # Libraries loaded and some basic functions defined paralpha <- function(imean, ivar) imean * (imean * (1 - imean) / ivar - 1) # beta distribution parameters parbeta <- function(imean, ivar) (1 - imean) * (imean * (1 - imean) / ivar - 1) library(OpasnetBaseUtils) library(MASS) library(ggplot2) # Common variable generation n <- 1000 tlcf <- data.frame(obs = 1:n, Result=rbeta(n, paralpha(0.2, 0.1^2), parbeta(0.2, 0.1^2))) #ggplot(tlcf, aes(x=Result)) + geom_density() #tlcf <- data.frame(Result = 0.1) tsfp <- sfp() #test2 <- data.frame(obs = 1:n, Result=rbeta(n, paralpha(0.2, 0.2^2+0.01), parbeta(0.2, 0.2^2+0.01))) #ggplot(test2, aes(x=Result)) + geom_density() # Default, model based on current knowledge test <- op_baseGetData("opasnet_base", "Op_en4926") temp2 <- as.data.frame(as.table(apply(tapply(test$Result, test[,c("Age","Scenario","Outcome")], mean), c(2,3), sum))) ggplot(temp2, aes(x = Outcome, weight = Freq, fill = Scenario)) + geom_bar(position = "dodge") temp <- op_baseGetData("opasnet_base", "Op_en4925")[,-c(1,2)] tvac_cov <- data.frame(temp, Scenario = "vacscenario") tvac_cov <- rbind(tvac_cov, data.frame(Age=tvac_cov[,"Age"], Result = 0, Scenario = "novacscenario")) temp[2:4,2] <- 0 tvac_cov <- rbind(tvac_cov, data.frame(temp, Scenario = "5-19novac")) test <- outcome(inarc = narc(ivac_cov = tvac_cov), sf(isfp = tsfp, iimm = imm(ivac_cov = tvac_cov))) temp <- as.data.frame(as.table(tapply(test$Result, test[,c("obs","Scenario")], sum))) ggplot(temp, aes(x = Freq, fill = Scenario)) + geom_density(alpha = 0.2) tapply(temp$Freq, temp[,c("Scenario")], mean) #op_baseWrite("opasnet_base", test) # Sensitivity and value of information analysis #test <- op_baseGetData("opasnet_base", "Op_en4926") temp2 <- as.data.frame(as.table(tapply(test$Result, test[,(colnames(test)%in%c("Result","Outcome"))==FALSE], sum))) tNERF <- op_baseGetData("opasnet_base", "Op_en4923")[,-c(1)] colnames(tNERF)[colnames(tNERF)=="Result"] <- "tNERF" colnames(tlcf)[colnames(tlcf)=="Result"] <- "tlcf"#tlcf from above colnames(tsfp)[colnames(tsfp)=="Result"] <- "tsfp"#tsfp from above temp2 <- merge(temp2, tNERF) temp2 <- merge(temp2, tlcf) temp2 <- merge(temp2, tsfp) temp2$NERFbin <- cut(temp2$tNERF, c(-Inf, 1, quantile(temp2$tNERF[temp2$tNERF>1], 1:9/10), Inf)) temp2$lcfbin <- cut(temp2$tlcf, c(-Inf, quantile(temp2$tlcf, 1:9/10), Inf)) temp2$sfpbin <- cut(temp2$tsfp, c(-Inf, quantile(temp2$tsfp, 1:9/10), Inf)) temp3 <- as.data.frame(as.table(tapply(temp2$Freq, temp2[,(colnames(temp2)%in%c("Freq","obs","tNERF","tlcf","tsfp", "lcfbin","sfpbin"))==FALSE], mean))) colnames(temp3)[ncol(temp3)] <- "EogNERF" temp2 <- merge(temp2, temp3) temp3 <- as.data.frame(as.table(tapply(temp2$Freq, temp2[,(colnames(temp2)%in%c("Freq","obs","tNERF","tlcf","tsfp", "NERFbin","sfpbin","EogNERF"))==FALSE], mean))) colnames(temp3)[ncol(temp3)] <- "Eoglcf" temp2 <- merge(temp2, temp3) temp3 <- as.data.frame(as.table(tapply(temp2$Freq, temp2[,(colnames(temp2)%in%c("Freq","obs","tNERF","tlcf","tsfp", "lcfbin","NERFbin","EogNERF","Eoglcf"))==FALSE], mean))) colnames(temp3)[ncol(temp3)] <- "Eogsfp" temp2 <- merge(temp2, temp3) ## Correlation cor(temp2$Freq, temp2[,c("tNERF", "tlcf", "tsfp")], method = "spearman") ## EVPI mean(tapply(temp$Freq, temp$obs, min)) - min(tapply(temp$Freq, temp$Scenario, mean)) # not considering by age group mean(apply(tapply(temp2$Freq, temp2[,c("obs","Age")], min), 1, sum)) - sum(apply(tapply(temp2$Freq, temp2[,c("Scenario","Age")], mean), 2, min)) ## EVXPI for NERF, lcf and sfp mean(apply(tapply(temp2$EogNERF, temp2[,(colnames(temp2)%in%c("Freq","Scenario","tNERF","tlcf","tsfp","NERFbin","lcfbin","sfpbin", "EogNERF","Eoglcf","Eogsfp"))==FALSE], min), 2, sum)) - sum(apply(tapply(temp2$Freq, temp2[,c("Scenario","Age")], mean), 2, min)) mean(apply(tapply(temp2$Eoglcf, temp2[,(colnames(temp2)%in%c("Freq","Scenario","tNERF","tlcf","tsfp","NERFbin","lcfbin","sfpbin", "EogNERF","Eoglcf","Eogsfp"))==FALSE], min), 2, sum)) - sum(apply(tapply(temp2$Freq, temp2[,c("Scenario","Age")], mean), 2, min)) mean(apply(tapply(temp2$Eogsfp, temp2[,(colnames(temp2)%in%c("Freq","Scenario","tNERF","tlcf","tsfp","NERFbin","lcfbin","sfpbin", "EogNERF","Eoglcf","Eogsfp"))==FALSE], min), 2, sum)) - sum(apply(tapply(temp2$Freq, temp2[,c("Scenario","Age")], mean), 2, min)) #vacscenario <- outcome() #novacscenario <- outcome(inarc = narc(ivac_cov=data.frame(Result=0)), sf(iimm=imm(ivac_cov=data.frame(Result=0)))) #temp <- as.data.frame(as.table(tapply(vacscenario$Result, vacscenario[,c("obs","Outcome")], sum))) #tapply(vacscenario$Result, vacscenario[,c("Age","Outcome")], mean) #tapply(temp$Freq, temp$Outcome, mean) #ggplot(temp, aes(x=Freq, fill=Outcome)) + geom_density(alpha = 0.2) #colnames(vacscenario)[ncol(vacscenario)] <- "vacscenario" #colnames(novacscenario)[ncol(novacscenario)] <- "novacscenario" #fout <- merge(vacscenario, novacscenario) #fout <- reshape(fout, idvar = names(fout)[(names(fout)%in%c("vacscenario","novacscenario"))==FALSE], times = c("vacscenario","novacscenario"), # timevar = "Scenario", varying = list(c("vacscenario","novacscenario")), direction = "long") #colnames(fout)[ncol(fout)] <- "Result" #temp <- as.data.frame(as.table(tapply(fout$Result, fout[,c("obs","Scenario")], sum))) #ggplot(temp, aes(x = Freq, fill = Scenario)) + geom_density(alpha = 0.2)